矩阵25码(Matrix 2 of 5)
什么是矩阵25码
矩阵25码(Matrix 2 of 5,也称为Code 2 of 5 Matrix)是一种可变长度、离散、条(或空)两种宽度的条码。矩阵25码是25码系列的子集。与工业25码(Industrial 2 of 5)不同,矩阵25码不仅可以用条编码数据,还可以用空编码数据。
矩阵25码由荷兰的Nieaf Company于1970年代开发,通常用于仓库分类、照片整理和机票标记。
矩阵25码只能编码数字0-9。矩阵2 of 5可以包括可选的校验符。大多数条码阅读器都支持这种条码。
矩阵25码的编码规则
矩阵25码是25码系列的子集,使用宽和窄元素进行编码。与之前开发的工业25码(Industrial 2 of 5)不同,它同时使用条和空进行数据编码。但是,它的密度低于交叉25码(Interleaved 2 of 5),因为它是离散的条码并且需要数据模式之间的额外空间。与交叉25码(Interleaved 2 of 5)相比的主要优势是能够对奇数个字符进行编码。
矩阵25码使用三个条和两个空编码从0到9的数字,每个数据模式都由额外的间隙(Gap)隔开。矩阵2 of 5可以包括添加到条形码末尾的可选校验符。
下面是字符编码表
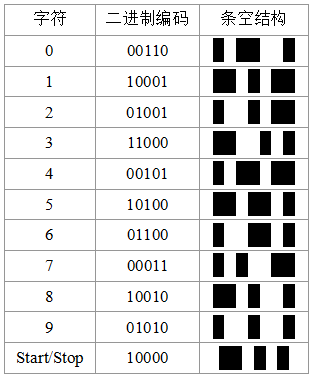
矩阵25码特点:
(1)字符集是0-9的数字;
(2)编码密度适中:条形码长度比Interleaved 2 of 5符号系统长11%,比Code 128 长82%;
(3)可变长度;
(4)可以包括可选的校验码;
(5)条码中的四个起始条和空格具有自己的权重,用于编码符号的值(零除外)。此外,最后一个条用作奇偶校验位以避免错误。符号的值是四个第一模式元素的非零权重之和。
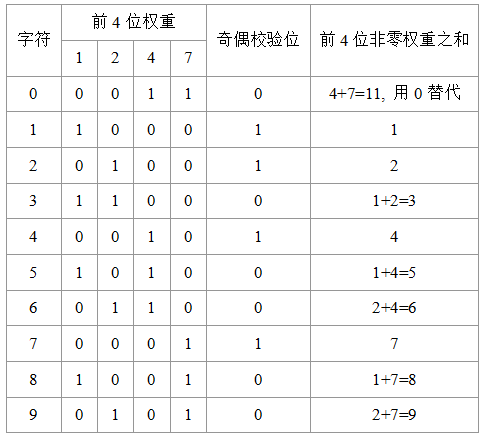
宽条或宽空的宽度是窄条或窄空2至3倍
矩阵25码的组成结构
矩阵25码具有以下结构:
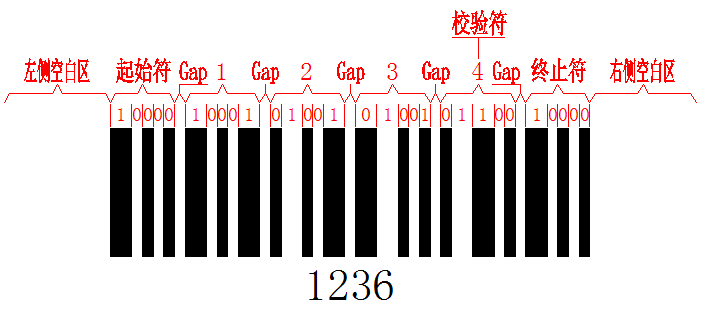
• 左侧空白区
• 起始符
• 字符间的间隙(Gap)
• 可变长度数据符
• 可选的校验符
• 终止符
• 右侧空白区
左、右侧空白区宽度至少为窄条或窄空的10倍。
矩阵25码的校验符及其计算方法
矩阵25码可包括一个可选的校验符,它基于mod 10算法,计算方式与工业25码相同。
下面以6位数字123456 为例介绍校验符计算方法:
(1)奇数位相加乘以3:(6+4+2)*3=36;
(2)偶数位相加:5+3+1=9;
(3)前两步骤的结果相加,然后对10取余:(36+5)mod10=5;
(4)用10减去步骤3的结果,即为校验符(如结果为10,刚以0代替):10-5=5,即校验符为5。
Matrix 2 of 5 条形码偶尔用于仓库应用,但其他选项(例如 Industry 2 of 5、Interleaved 2 of 5 或 ITF-14/SCC-1)通常是首选,因为它们提高了可读性和准确性。 虽然 Matrix 2 of 5 代码具有提高信息密度的优势,但与更常见的 2 of 5 条码集相比,该类型没有提供任何其他显著优势。


